Optimizing Datalog for the GPU

Datalog primer and a neat data structure

Optimizing Datalog for the GPU Yihao Sun, Ahmedur Rahman Shovon, Thomas Gilray, Sidharth Kumar, and Kristopher Micinski ASPLOS'25

Datalog Primer

Datalog source code comprises a set of relations, and a set of rules.

A relation can be explicitly defined with a set of tuples. A running example in the paper is to define a graph with a relation named edge:

Edge(0, 1)
Edge(1, 3)
Edge(0, 2)

A relation can also be implicitly defined with a set of rules. The paper uses the Same Generation (SG) relation as an example:

1: SG(x, y) <- Edge(p, x), Edge(p, y), x != y
2: SG(x, y) <- Edge(a, x), SG(a, b), Edge(b, y), x != y

Rule 1 states that two vertices (x and y) are part of the same generation if they both share a common ancestor (p), and they are not actually the same vertex (x != y).

Rule 2 states that two vertices (x and y) are part of the same generation if they have ancestors (a and b) from the same generation.

“Running a Datalog program” entails evaluating all rules until a fixed point is reached (no more tuples are added).

Semi-naïve Evaluation

One key idea to internalize is that evaluating a Datalog rule is equivalent to performing a SQL join. For example, rule 1 is equivalent to joining the Edge relation with itself, using p as the join key, and (x != y) as a filter.

Semi-naïve Evaluation is an algorithm for performing these joins until convergence, while not wasting too much effort on redundant work. The tuples in a relation are put into three buckets:

1. new: holds tuples that were discovered on the current iteration

2. delta: holds tuples which were added in the previous iteration

3. full: holds all tuples that have been found in any iteration

For a join involving two relations (A and B), new is computed as the union of the result of 3 joins:

1. delta(A) joined with full(B)

2. full(A) joined with delta(B)

3. delta(A) joined with delta(B)

The key fact for performance is that full(A) is never joined with full(B).

More details on Semi-naïve Evaluation can be found in these notes.

Hash-Indexed Sorted Array

This paper introduces the hash-indexed sorted array for storing relations while executing Semi-naïve Evaluation on a GPU. It seems to me like this data structure would work well on other chips too. Fig. 2 illustrates the data structure (join keys are in red):

Source: https://dl.acm.org/doi/10.1145/3669940.3707274

The data array holds the actual tuple data. It is densely packed in row-major order.

The sorted index array holds pointers into the data array (one pointer per tuple). These pointers are lexicographically sorted (join keys take higher priority in the sort).

The hash table is an open-addressed hash table which maps a hash of the join keys to the first element in the sorted index array that contains those join keys.

A join of relations A and B, can be implemented with the following pseudo-code:

for each tuple 'a' in the sorted index array of A:

  lookup (hash table) the first tuple in B which has matching join keys to 'a'

  iterate over all tuples in the sorted index array of B with matching keys

Memory accesses when probing through the sorted index array are coherent. Memory accesses when accessing the data array are coherent up to the number of elements in a tuple.

Results

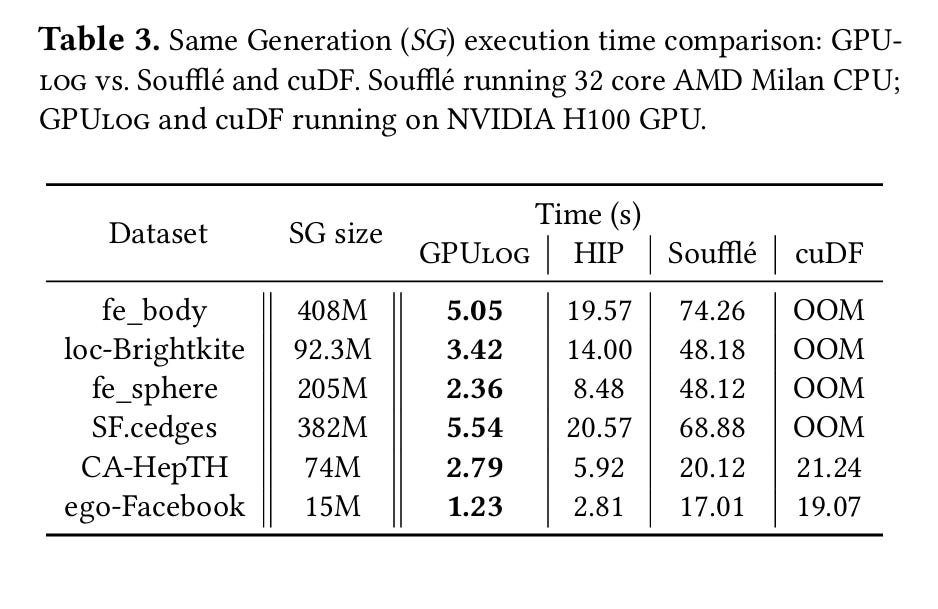
Table 3 compares the results from this paper (GPULog) against a state-of-the-art CPU implementation (Soufflé). HIP represents GPULog ported to AMD’s HIP runtime and then run on the same Nvidia GPU.

Source: https://dl.acm.org/doi/10.1145/3669940.3707274

Dangling Pointers

The data structure and algorithms described by this paper seem generic, it would be interesting to see them run on other chips (FPGA, DPU, CPU, HPC cluster).

I would guess most of GPULog is bound by memory bandwidth, not compute. I wonder if there are Datalog-specific algorithms to reduce the bandwidth/compute ratio.