SPID-Join
SPID-Join: A Skew-resistant Processing-in-DIMM Join Algorithm Exploiting the Bank- and Rank-level Parallelisms of DIMMs Suhyun Lee et al., SIGMOD'24
In-DIMM Processors
Before reading this paper, I thought of processing-in-memory as something that will arrive in the future, but now I realize it may come sooner than I thought. When a paper quotes the MSRP of a product ($300/DIMM) then it cannot be that far-fetched. The system described in this paper uses UPMEM (acquired by Qualcomm) DIMMs. The paper mentions Samsung AxDIMM as an alternative.
Each bank in a UPMEM DIMM is associated with an In-DIMM Processor (IDP) which is a multi-threaded, in-order core that can run user code, but it can only access data stored in the associated bank (and a 64KiB working memory). The fundamental performance advantage here is that the aggregate memory bandwidth available to all IDPs is higher (4-5x) than the memory bandwidth available to the host CPU.
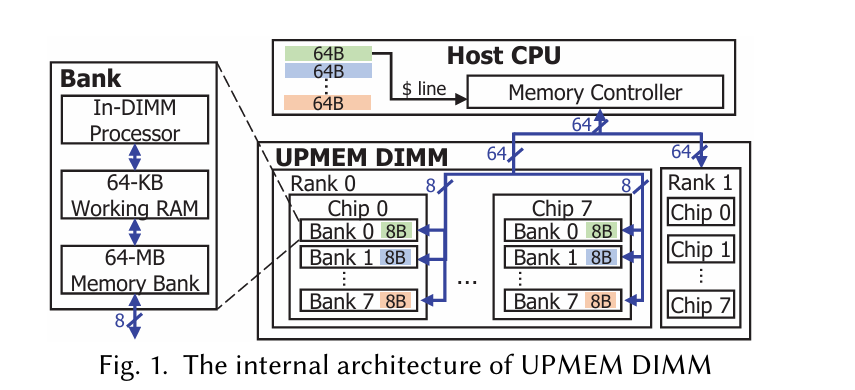
The system described in the paper has a host CPU with access to both vanilla DDR4 DIMMs and 8 UPMEM DIMMs.
Two Join Properties
Here are two divide-and-conquer properties from relational algebra which are helpful in understanding this paper:
Where the relation (i.e., table) B has been divided into subsets B0 and B1. In practical terms, this means that if A is relatively small, you can parallelize this join by parallelizing over subsets of B.
Here, both A and B have both been partitioned into smaller relations. In other words, to partition A into N partitions, iterate over each tuple in A and compute a log2(N)-bit-wide hash of the join key(s). That hash value is the index of the target partition for the current tuple.
This property describes a two-step partitioned join. In step one, both tables are partitioned into N partitions according to the join key(s). In step two, N partition-wise joins are executed. Both steps can be parallelized.
PID-Join
This paper builds on prior work which implements in-memory joins, the algorithm is called PID-Join. PID-Join operates on two tables: R and S. R is assumed to be smaller than S and contains unique join keys. PID-Join is simply a partitioned join, where each IDP processes a separate partition.
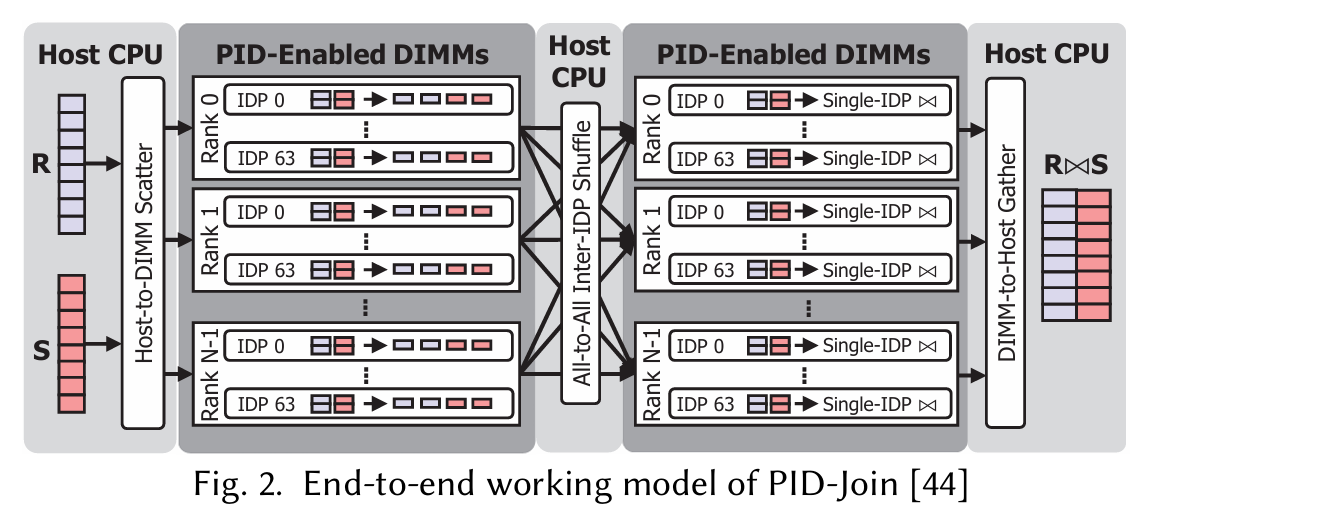
PID-Join assumes that the host CPU has access to R and S (either in DDR4 or realized on demand). Say the number of IDPs is N. PID-Join performs the following steps:
The host writes subsets of R and S to UPMEM banks such that the rows are evenly distributed among banks (and hence IDPs). Note that this is not partitioning, but rather arbitrarily dividing rows among banks.
Each IDP partitions the rows that were assigned to it into N partitions.
The host CPU shuffles data between IDPs such that each IDP receives 1 partition of both R and S.
Each IDP can then optionally further partition its local partitions. This is used to ensure that the working set in the next step can fit into IDP-local working memory.
Each IDP performs a join (e.g., a hash join or a sort-merge join) on its local partition(s).
SPID-Join
Skewed data causes load imbalances for PID-Join. For example, consider the extreme case where one specific join key occurs much more frequently than all others. Then the IDP which handles that join key will be the long pole in the tent because the partition assigned to it will be disproportionally large.
SPID-Join resolves this by grouping multiple IDPs together into a single set. A set of IDPs receives a single partition. For example, set i receives Ri and Si. Ri is replicated among all IDPs in the set, while is Si is evenly distributed among them.
There is a tradeoff here: larger set sizes reduce load imbalance, but increase the amount of time the system spends performing redundant computations on R. Section 4.4 describes techniques to look at statistics of R and S to determine the ideal IDP set size for a given query.
Results
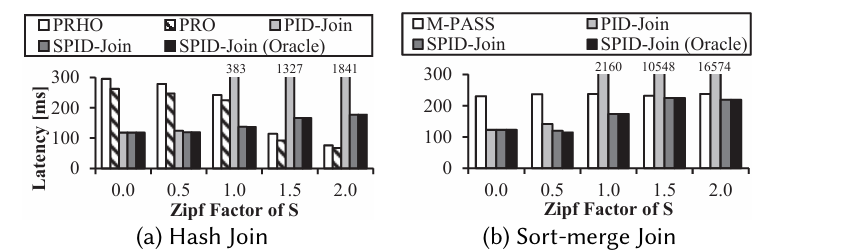
The Zipf Factor on the x-axis here is a measure of how skewed the data is. PRHO, PRO, and M-PASS are CPU join implementations. The (Oracle) version picks the ideal IDP set configuration based on offline profiling.
Dangling Pointers
The host-scattering step followed by the IDP partitioning here seems redundant. Is there a reason the host can’t do the initial coarse-grained partitioning when it writes data into each IDP initially? Maybe TLB misses become a problem if the number of partitions is too large.
The fact that there is no inter-IDP communication available beyond host reads and writes seems like a problem for many applications. I wonder if the next logic step is some sort of network which connects the IDPs (RDMA between IDPs?)
It would be great to see this extended to handle more query operators rather than just the join, ideally the input data could be resident in UPDIMMs at the start of the query.

